| |
Tritone Paradox
The Tritone Paradox was discovered by Deutsch in 1986, first reported at a meeting of the Acoustical Society of America (Deutsch, 1986)1, and first published in Deutsch, Music Perception (1986)2.
The basic pattern that produces this illusion consists of two computer-produced tones that are related by a half-octave. (This interval is called a tritone). When one tone of a pair is played, followed by the second, some people hear an ascending pattern. But other people, on listening to the identical pair of tones, hear a descending pattern instead. This experience can be particularly astonishing to a group of musicians who are all quite certain of their judgments, and yet disagree completely as to whether such a pair of tones is moving up or down in pitch.
The Tritone Paradox has another curious feature. In general, when a melody is played in one key, and it is then transposed to a different key, the perceived relations between the tones are unchanged. The notion that a melody might change shape when it is transposed from one key to another seems as paradoxical as the notion that a circle might turn into a square when it is shifted to a different position in space.
But the Tritone Paradox violates this rule. When one of these tone pairs is played (such as C followed by F#) a listener might hear a descending pattern. Yet when a different tone pair is played (such as G# followed by D), the same listener hears an ascending pattern instead. (Another listener might hear the C-F# pattern as ascending and hear the G#-D pattern as descending.) 1 - 3
The following sound demonstration presents four tritone pairs. When you listen to each pair of tones, decide whether it forms an ascending pattern or a descending one. This demonstration works best when you play the tones to a group of listeners. After presenting each tritone pair, ask the listeners for a show of hands (‘Do you hear this pattern as ascending?’ ‘Do you hear it as descending?’). You will most probably find that the listeners disagree amongst themselves as to which pair of tones is ascending, and which is descending in pitch. This is particularly surprising when the demonstration is played to a group of musicians who are all certain of their judgments.
 Listen to four examples of Deutsch's Tritone Paradox Listen to four examples of Deutsch's Tritone Paradox
The tones that are employed to create the Tritone Paradox are so constructed that their note names (C, C#, D and so on) are clearly defined, but they are ambiguous with respect to which octave they are in. For example, one tone might clearly be a C, but in principle it could be middle C, or the C an octave above, or the C an octave below. This ambiguity is built into the tones themselves. So when someone is asked to judge, for example, whether the pair of tones D-G# is ascending or descending in pitch, there is literally no right or wrong answer. Whether the tones appear to move up or down in pitch depends entirely on the mind of the listener. (Ambiguous tones such as these were used by Roger Shepard and Jean-Claude Risset to create illusions of endlessly ascending or descending pitches.)
The way that any one listener hears the Tritone Paradox depends on the names of the notes that are played. The musical scale is created by dividing the octave into twelve semitone steps, and each tone is given a name: C, C#, D, D#, E, F, F#, G, G#, A, A# and B. The entire scale, as it ascends in height, consists of the repeating occurrence of this succession of note names across octaves. So when you move up a piano keyboard in semitone steps beginning on C, you go first to C#, then D, then D#, and so on, until you get to A#, then B, and then C again. At this point you have reached an octave, and you begin all over, repeating the same series of note names in the next octave up the keyboard.
Because all Cs sound in a sense equivalent, as do all C#s, all Ds, and so on, we can think of pitch as varying both along a simple dimension of height and also along a circular dimension of pitch class - a term that musicians use to describe note names. So, for example, all Cs are in pitch class C, all C#s are in pitch class C#, and all Ds are in pitch class D.
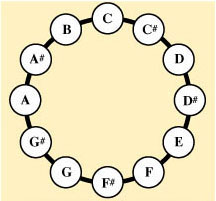
| Figure 1. The pitch class circle. This corresponds to the twelve pitch classes within the octave. In experiments on the Tritone Paradox, pairs of tones are played that are opposite each other along the circle, such as C-F#, or G#-D. |
Let us suppose that listeners mentally arrange pitch classes as a circular map, like a clockface, as shown in Figure 1. To explain different listeners' perceptions of the Tritone Paradox, I conjectured that one person might orient his or her clockface so that C is in the 12 o'clock position, C# is in the 1 o'clock position, and so on around the circle. This listener would tend to hear the pattern C-F# (as well as B-F, and C#-G) as descending, and the pattern F#-C (as well as F-B and G-C#) as ascending. But another person might orient is or her clockface so that F# is in the 12 o'clock position, G is in the 1 o'clock position, and so on. This listener would instead tend to hear the pattern C-F# (as well as B-F, and C#-G) as ascending, and the pattern F#-C (as well as F-B and G-C#) as descending. In other words, differences between listeners in perception of the Tritone Paradox could be due to differences in the way they orient their maps of the pitch class circle.3
In one experiment, I played many such pairs of tones to a group of subjects, and they judged in each case whether they heard an ascending or a descending pattern. I then plotted the proportion of times that each subject heard a descending pattern, as a function of the pitch class of the first tone of the pair. The results supported my conjecture - the judgments of most subjects varied systematically depending on the positions of the tones along the pitch class circle: Tones in one region of the circle tended to be heard as higher, and tones in the opposite region as lower.
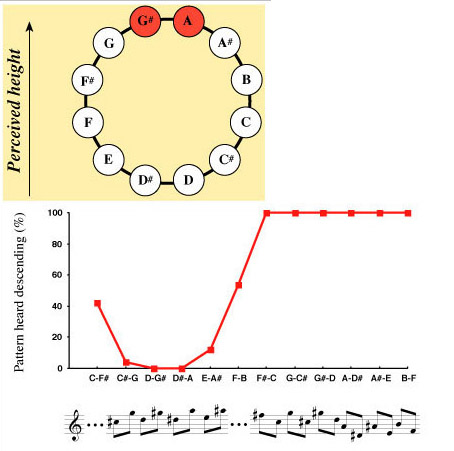
| Figure 2. Perception of the Tritone Paradox by a subject who perceived the illusion in a pronounced fashion. The upper figure shows the orientation of the pitch class circle with respect to height, derived from the judgments of the subject shown in the graph. This subject’s peak pitch classes were G# and A. |
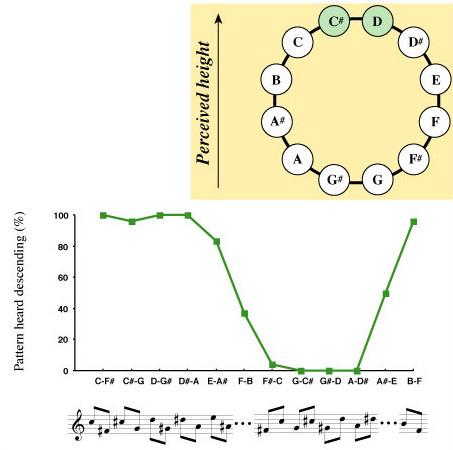
In addition, the orientation of the pitch class circle varied strikingly from one subject to another. To illustrate these differences, the judgments of two subjects are shown in Figures 2 and 3. Both these subjects heard the Tritone Paradox in a very pronounced fashion, but quite differently from each other. The subject whose judgments are shown in Figure 2 heard tone pairs C#-G, D-G#, D#-A and E-A# as ascending, but F#-C, G-C#, G#-D, A-D#, A#-E, and B-F as descending. In contrast, the subject whose judgments are shown in Figure 3 heard tone pairs B-F, C-F#, C#-G, D-G#, D#-A, and E-A# as descending, and F#-C, G-C#, G#-D, and A-D# as ascending. So for the most part when the first subject heard an ascending pattern the second subject heard a descending one, and vice versa. The upper parts of the figures show the two orientations of the pitch class circle with respect to height which were derived from the judgments of these subjects. For the first subject, pitch classes G# and A stood at the top of the circle, but for the second subject, C# and D stood in this position instead. To further illustrate the differences between listeners in perception of the Tritone Paradox, the judgments of four more subjects are shown in Figure 4.
|
Figure 3. Perception of the Tritone Paradox by another subject who perceived it in a pronounced fashion, but quite differently from the first subject. The upper figure shows the orientation of the pitch class circle with respect to height, derived from the judgments of the subject shown in the graph. This subject’s peak pitch classes were C# and D.
|
Another surprising consequence of the Tritone Paradox concerns absolute pitch - the ability to name a note in the absence of a reference note. This ability is generally considered to be very rare. But the Tritone Paradox shows that the large majority of people possess an implicit form of absolute pitch, since on listening to this pattern they hear tones as higher or as lower depending simply on their pitch classes, or note names.

| Figure 4. Perception of the Tritone Paradox by four more subjects. |
Why do people orient their maps of the pitch class circle in different ways? I conjectured that the answer might lie in the speech patterns that we hear. When people from other countries visited my laboratory in California, they often heard this pattern differently from native Californians. And when I demonstrated the effect to audiences in other countries, they appeared to differ from one country to another in what they heard.
So on the basis of these observations, I compared two groups of subjects. One group had grown up in California, and the other group had grown up in the south of England. As shown in Figure 5, these two groups differed strikingly in how they heard the Tritone Paradox: Frequently when a Californian subject heard a pattern as ascending, a subject from the south of England heard the identical pattern as descending, and vice versa4.
In another study, my colleagues and I found a significant correspondence between the pitch range of a person's speaking voice and how he or she perceived this pattern. This study provided a further indication that speech patterns influence the way the Tritone Paradox is heard5. Further, in an experiment described in the page entitled The pitch of speech in two Chinese villages my colleagues and I found that the pitch ranges of speech clustered within a linguistic community, but differed across communities. This is in line with the conjecture that the individual develops a pitch class template that is derived from the pitch ranges of speech to which he or she is most frequently exposed. This template then influences the pitch range of his or her own speech, and also influences how he or she hears the Tritone Paradox. The 2013 book chapter 6 provides further information and discussion of this effect.
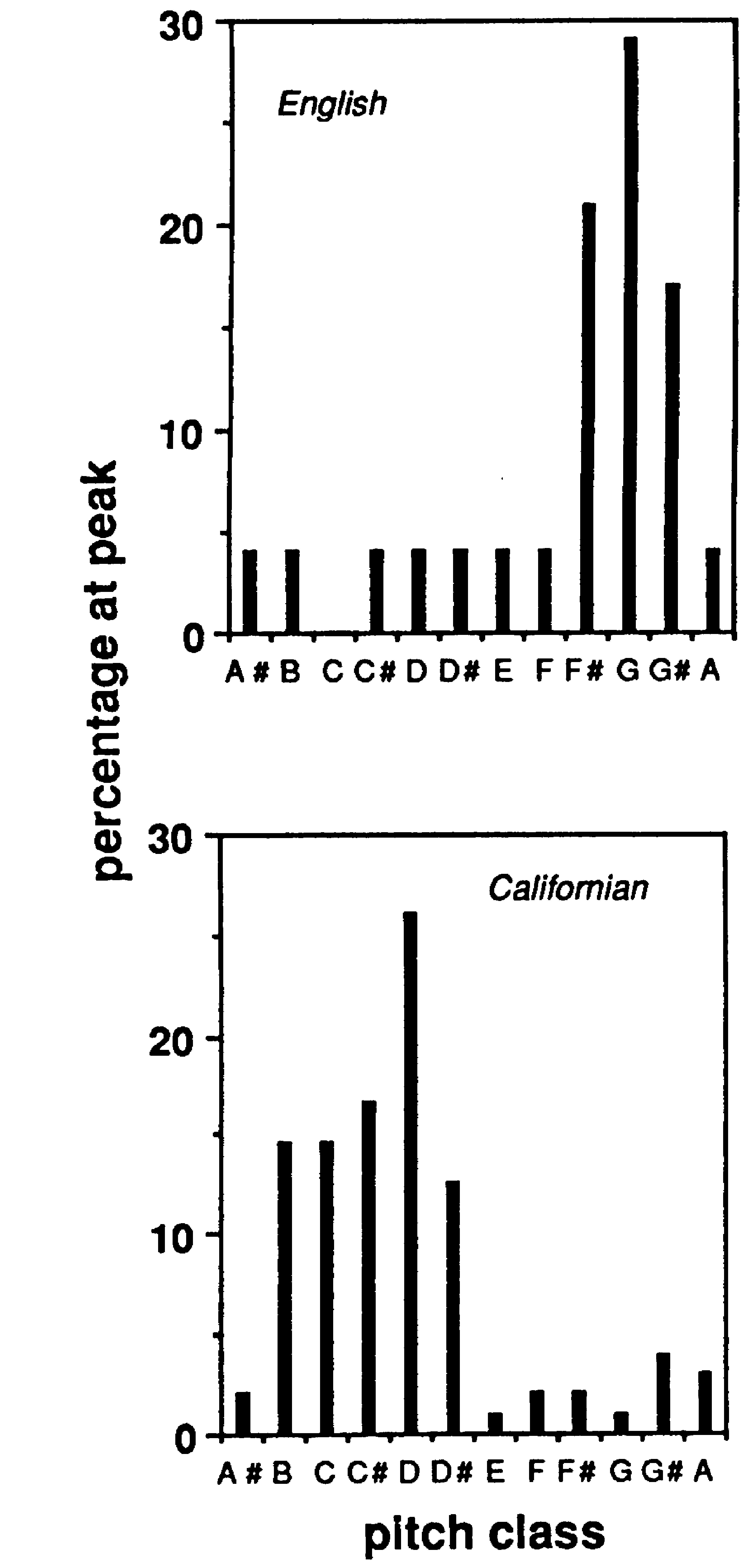
| Figure 5. Distributions of peak pitch classes in two groups of subjects. One group had grown up in the south of England, and the other group had grown up in California. The two groups heard the Tritone Paradox in strikingly different ways. |
Other studies have uncovered regional differences within the U.S. and Canada in the perception of the Tritone Paradox6. Because there are regional dialects within the U.S., it seems that speech patterns are likely to lie at the root of these differences also. It even appears that the way a person hears the Tritone Paradox is related, not only to the geographical region in which he or she had grown up, but also to the regions in which his or her parents had grown up. In one study we found that, among subjects who had grown up in the area of Youngstown, Ohio, the perceptions of those whose parents had also grown up in Youngstown differed significantly from those whose parents had grown up elsewhere in the U.S.7. In a further study, I found a significant correlation between the way children and their mothers heard the Tritone Paradox 8,9. This correlation was obtained even though the children had all been born and raised in California, whereas their mothers had grown up in many different geographical regions, both inside and outside the U.S.
Another study examined what happens when an individual had been exposed to one language in infancy and later acquired a different language. My colleagues and I tested subjects who had been born in Vietnam and now reside in California. One group had arrived in the U.S. as adults and spoke perfect Vietnamese but little English. The second group had arrived in the U.S. as infants or young children; they spoke perfect English, but most of them were not fluent speakers of Vietnamese. Figure 6 shows the distributions of peak pitch classes in the two Vietnamese groups combined, together with those of the subjects who had been born and raised in California and spoke only English. The two Vietnamese groups did not differ statistically in how they heard the Tritone Paradox, but both differed statistically from the native speakers of Californian English.10 This leads to the conclusion that the speech to which we were exposed as children influences the way we hear the Tritone Paradox as adults.
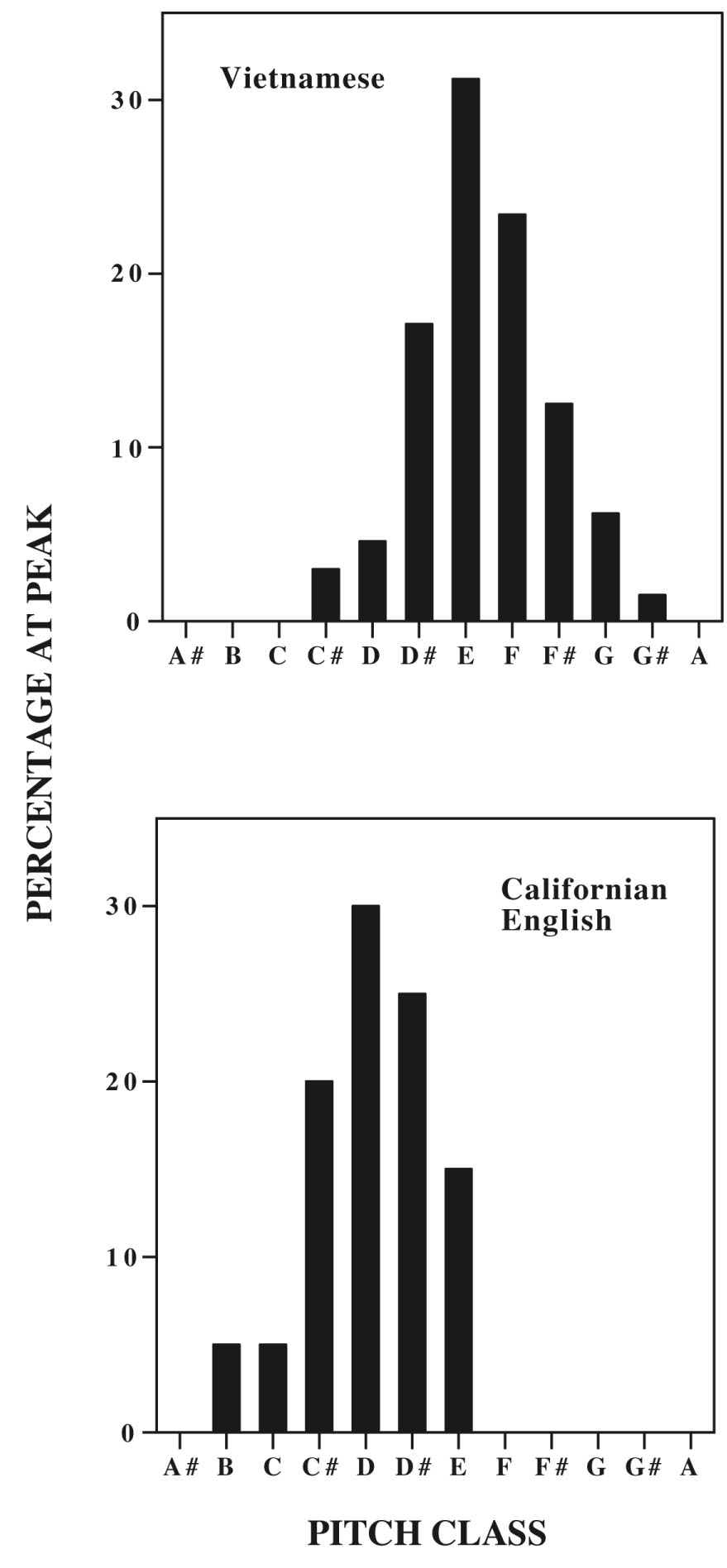
| Figure 6. Distributions of peak pitch classes among subjects who had been born in Vietnam and whose first language was Vietnamese, and among subjects who were native speakers of Californian English. |
References 11-15 provide further information about the Tritone Paradox. The sound patterns for a full experiment on the illusion, together with instructions as to how to score the answers, are published in the compact disc 'Musical Illusions and Paradoxes.'
This strange illusion has implications for the relationship between speech and music. Philosophers and composers have argued for centuries that strong linkages must exist between these two forms of communication. Indeed, many composers, in their search for expressivity, have incorporated into their music features that are characteristic of spoken language. The Tritone Paradox shows that the speech patterns to which we have been exposed can indeed influence how music is perceived.
References:
1. Deutsch, D. An auditory paradox. Journal of the Acoustical Society of America, 1986, 80, s93. [Web Link]
2. Deutsch, D. A musical paradox. Music Perception, 1986, 3, 275-280. [PDF Document]
3. Deutsch, D. Paradoxes of musical pitch. Scientific American, 1992, 267, 88-95, [PDF Document]
4. Deutsch, D. The tritone paradox: An influence of language on music perception. Music Perception, 1991, 8, 335-347. [PDF Document]
5. Deutsch, D., North, T. and Ray, L. The tritone paradox: Correlate with the listener's vocal range for speech. Music Perception, 1990, 7, 371-384. [PDF Document]
6. Deutsch, D. The processing of pitch combinations In D. Deutsch (Ed.). The psychology of music, 3rd Edition, 2013, 249-325, San Diego: Elsevier. [PDF Document] [Web Link]
7. Ragozzine, F. and Deutsch, D. A regional difference in perception of the tritone paradox within the United States. Music Perception, 1994, 12, 213-225. [PDF Document]
8. Deutsch, D. Mothers and their children hear a musical illusion in strikingly similar ways. Invited Lay language paper presented at the 131st meeting of the Acoustical Society of America. 1996, May, Indianapolis. [Laylanguage version]
9. Deutsch, D. Mothers and their offspring perceive the tritone paradox in closely similar ways. Archives of Acoustics, 2007, 32, 3-14. [PDF Document]
10. Deutsch, D., Henthorn T. and Dolson, M. Speech patterns heard early in life influence later perception of the tritone paradox. Music Perception, 2004, 21, 357-372. [PDF Document]
11. Deutsch, D. The tritone paradox: A link between music and speech. Current Directions in Psychological Science, 1997, 6, 174-180. [PDF Document]
12. Deutsch, D. The tritone paradox: Some further geographical correlates. Music Perception, 1994, 12, 125-136. [PDF Document]
13. Deutsch, D. Some new pitch paradoxes and their implications. In Auditory Processing of Complex Sounds. Philosphical Transactions of the Royal Society, Series B, 1992, 336, 391-397. [PDF Document]
14. Deutsch, D., Kuyper, W. L. and Fisher, Y. The tritone paradox: Its presence and form of distribution in a general population. Music Perception, 1987, 5, 79-92. [PDF Document]
15. Deutsch, D. The tritone paradox: Effects of spectral variables. Perception & Psychophysics, 1987, 41, 563-575. [PDF Document]
16. Deutsch, D. (Ed.). The processing pf pitch combinations. Chapter 7 in The Psychology of Music, 3rd Edition, San Diego: Elsevier, 2013.
17. Deutsch, D. The Tritone Paradox: An Influence of Speech on how Music is Perceived. Chapter 7 in Musical Illusions and Phantom Words: How Music and Speech Unlock Mysteries of the Brain, Oxford University Press. 2019,
18. Deutsch, D. The Tritone Paradox: An Influence of Speech on how Music is Perceived. Chapter 7 in Musical Illusions and Phantom Words: How Music and Speech Unlock Mysteries of the Brain, Korean translation, Eidos Publishing Group, 2023.
19. Deutsch, D. The Tritone Paradox: An Influence of Speech on how Music is Perceived. Chapter 7 in Musical Illusions and Phantom Words: How Music and Speech Unlock Mysteries of the Brain, Chinese translation, Guangxi Normal University Press, Group Co, Ltd, 2024.

| |