| |
Pitch Circularity
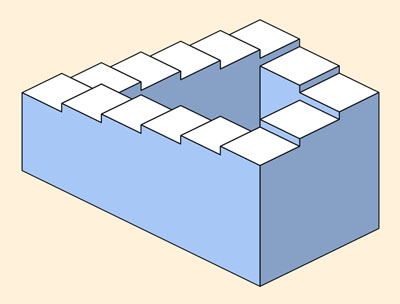
The figure on the left below represents an impossible staircase, similar to one originally published by Penrose and Penrose in 19581. Since each stair that is one step clockwise from its neighbor is also one step downward, the staircase appears to be eternally descending. Our perceptual system insists on this interpretation, even though it cannot be correct.
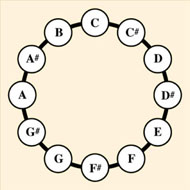
Pitch circularities are based on the same principle. By analogy with real world staircases, pitch is generally viewed as extending along a scale from low to high, as can be experienced by sweeping one’s hand up a keyboard. But pitch also has a circular component, known as pitch class. This is acknowledged in our musical scale, which is based on the circular configuration shown on the right below. As we ascend this scale in semitone steps, we repeatedly traverse the pitch class circle in clockwise direction, so that we play C, C#, D, and so on all around the circle, until we reach A, A#, B - and then we proceed to C, C#, D again, and so on.
 |
 |
An impossible staircase, similar to the one
devised by Penrose and Penrose. |
The pitch class circle |
To accommodate both the linear and circular dimensions, music theorists have suggested that pitch should be represented as a helix having one complete turn per octave, so that tones that are separated by octaves are also close on this representation, as shown below.
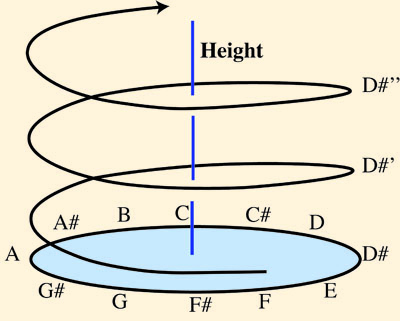
The helical model of pitch
Shepard (1964)2 reasoned that by creating banks of tones whose note names (pitch classes) are clearly defined but whose perceived heights are ambiguous, the helix could be collapsed into a circle, so enabling the creation of scales that ascend or descend endlessly in pitch. He achieved this ambiguity by creating banks of complex tones, with each tone consisting only of components that were separated by octaves, and whose amplitudes were scaled by a fixed bell-shaped spectral envelope. Such tones are well defined in terms of pitch class, but poorly defined in terms of height. When such tones are played traversing the pitch class circle in clockwise direction, one obtains the impression of an eternally ascending scale– C# is heard as higher than C; D as higher than C#; D# as higher than D; . . . . A# as higher than A; B, as higher than A#; C as higher then B – and so on endlessly. Counterclockwise movement creates the impression of an eternally descending scale. Risset (1971)3 has created intriguing variants using gliding tones that appear to ascend or descend continuously in pitch. See the review by Deutsch (1992)4 for details.
Later, I reasoned that it should be possible to create circular scales from sequences of single tones, with each tone comprising a full harmonic series. If you take a harmonic complex tone and gradually reduce the amplitudes of the odd-numbered harmonics (1, 3, 5, etc.), keeping the amplitudes of the even-numbered harmonics (2, 4, 6, etc.) constant, the tone should appear to increase smoothly in height, while remaining in the same pitch class. In Sound Demo 1, a harmonic complex tone based on A4 (concert A) is presented, with the odd-numbered harmonics gradually gliding down in amplitude. At some point, listeners realize that they are hearing the note an octave higher – but this perceptual transition had occurred without the sounds traversing the semitone scale, but remaining on note A.
 Sound Demo 1
I further reasoned that we should be able to produce pitch circularities on this principle. We begin with a bank of twelve harmonic complex tones, whose fundamental frequencies range over an octave in semitone steps. For the tone with the highest fundamental, the odd and even harmonics are equal in amplitude. Then for the tone a semitone lower, the amplitudes of the odd harmonics are reduced relative to the even ones, so raising the perceived height of this tone. Then for the tone another semitone lower, the amplitudes of the odd harmonics are reduced further, so raising the perceived height of this tone to a greater extent. We continue down the octave in this way in semitone steps, until for the tone with the lowest fundamental, the odd-numbered harmonics no longer contribute to the tone’s perceived height. The tone with the lowest fundamental is therefore heard as displaced up an octave, and pitch circularity is achieved.
Here is an eternally descending scale based on this principle, with the amplitudes of the odd-numbered harmonics reduced by 3.5 dB for each semitone step down.
Sound Demo 2
And here is an eternally ascending scale based on the same principle:
Sound Demo 3
Here is an eternally descending glissando, based on the same principle:
Sound Demo 4
and here is an eternally ascending glissando, again based on this principle:
Sound Demo 5
Together with my colleagues, I carried out an experiment to determine whether such tones are indeed heard as circular, when all intervals are considered5. We created a bank of twelve tones, and from this bank we paired each tone sequentially with every other tone (e.g., tone pair C-C#; C-D; C-D#; and so on) creating 132 tone pairs altogether. Subjects judged for each pair whether it ascended or descended in pitch.
Here is an excerpt from the experiment, and you will probably find that your judgments of each pair correspond to the closest distance between the tones along the circle.
Sound Demo 6
When the subjects’ judgments were subjected to multidimensional scaling, strongly circular configurations were produced – as shown by the judgments from one subject below.
Multidimensional scaling solutions derived from subjects’ relative pitch judgments based on Deutsch’s circular scales
The finding that circular scales can be obtained from full harmonic series leads to the intriguing possibility that this algorithm could be used to transform banks of natural instrument tones so that they would also exhibit pitch circularity6. William Brent, then a graduate student at UCSD, has achieved considerable success using bassoon samples, and also some success with oboe, flute, and violin samples, and has shown that the effect is not destroyed by vibrato. The possibility of creating circular banks of tones derived from natural instruments expands the scope of musical materials available to composers and performers.
References:
1. Penrose, L. S., and Penrose, R. Impossible objects: A special type of visual illusion, British Journal of Psychology, 1958, 49, 31-33. (Unknown to the authors, Oscar Reutesvald had also created an impossible staircase in the 1930s.)
2. Shepard, R. N. Circularity in judgments of relative pitch, Journal of the Acoustical Society of America, 1964, 36, 2345–2353.
3. Risset, J. C. Paradoxes de hauteur, Proceedings of the 7th International Congress on Acoustics, 1971, Budapest, S10, 613-616.
4. Deutsch, D. Paradoxes of musical pitch. Scientific American, 1992, 267, 88-95, [PDF Document]
5. Deutsch, D., Dooley, K., and Henthorn, T. Pitch circularity from tones comprising full harmonic series. Journal of the Acoustical Society of America, 2008, 124, 589-597. [PDF Document]
6. Deutsch, D. The paradox of pitch circularity. Acoustics Today, 2010, July, 8-15. [PDF Document]
| |
